1. 조합
조합이 훨씬 쉽기 때문에 먼저 살펴본다.
개념 = [1, 0] 과 [0, 1] 을 동일한 원소로 판단한다. 즉 순서를 고려하지 않는다.

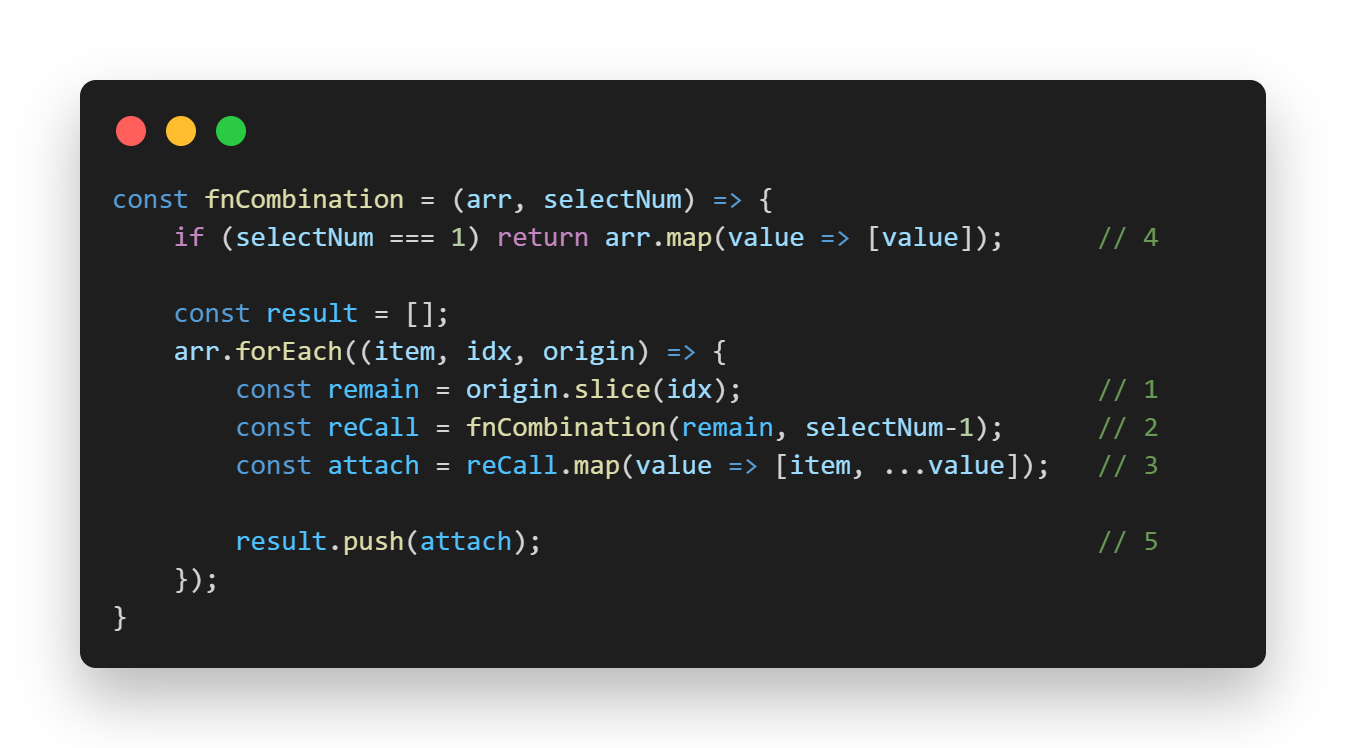
주석으로 기재한 숫자 순서대로 보면 이해가 쉽다.
쉬운 이해를 위해 fnCombination([1, 2, 3, 4], 3) 을 호출했다고 하자.
- arr = [1, 2, 3, 4] 의 첫 번째 요소인 item = 1 을 제외한 나머지를 새로운 배열로 생성한다. 여기서 origin 과 arr 은 동일한 배열이며 slice 함수는 첫 번째 파라미터로 주어진 인덱스 요소부터, 두 번째 파라미터로 주어진 인덱스 요소까지를 리턴하겠다는 의미이다. 두 번째 파라미터가 없을 경우 배열의 끝까지 리턴한다.
- 위에서 만든 새로운 배열 reamin = [2, 3, 4] 을 파라미터로 fnCombination 함수를 재호출한다. selectNum은 해당 배열에서 추출할 요소의 개수로, 현재 fnCombination 에서 첫 번째 요소로 item = 1 을 추출했으니, 기존에 추출하기로 했던 요소 3 에서 하나를 제외한 2를 파라미터로 할당한다.
- 1번과 2번 과정을 나타내보면 다음과 같다.
● [1] → (2, 3, 4) → [2] → (3, 4) →[3]
● [1] → (2, 3, 4) → [2] → (3, 4) →[4]
● [1] → (2, 3, 4) → [3] → (4) →[4]
● [2] → (3, 4) → [3] → (4) →[4]
여기서 ... 은 배열 자체가 아닌 배열의 요소만 저장하겠다는 의미이다. - 위의 내용을 최종적으로 result 변수에 저장한다.
2. 중복조합
[1, 2, 3] 중 2개를 추출하는 조합의 결과가 [1, 2] / [1, 3] / [2, 3] 이라면
중복 조합은 기존 조합의 결과에서 [1, 1] / [2, 2] / [3, 3] 이 추가된다.
간단하다. 기존의 조합에서 자기 자신을 제외한 나머지를 새롭게 배열로 만들었다면, 중복조합에서는 자기 자신을 포함시키면 된다. 즉 idx + 1 이 아닌 idx 부터 slice한 배열을 생성하면 된다. 이 때 생성되는 과정을 나타내보면 다음과 같다.
● [1] → (1, 2, 3, 4) → [1] → (1, 2, 3, 4) →[1]
● [1] → (1, 2, 3, 4) → [1] → (1, 2, 3, 4) →[2]
● [1] → (1, 2, 3, 4) → [1] → (1, 2, 3, 4) →[3]
● [1] → (1, 2, 3, 4) → [1] → (1, 2, 3, 4) →[4]
● [1] → (1, 2, 3, 4) → [2] → (2, 3, 4) →[3]
● [1] → (1, 2, 3, 4) → [2] → (2, 3, 4) →[4]
● [1] → (1, 2, 3, 4) → [3] → (3, 4) →[3]
● [1] → (1, 2, 3, 4) → [3] → (3, 4) →[4]
● [1] → (1, 2, 3, 4) → [4] → (4) →[4]
...
3. 순열
순열도 조합과 크게 다를 바 없다.
개념 = [1, 0] 과 [0, 1] 을 다른 원소로 판단한다. 즉 순서를 고려한다.

주석에 달린 숫자 순서대로 생각해보자.
이번에도 이해를 위해 fnPermutation([1, 2, 3], 2) 를 호출했다고 하겠다.
- arr = [1, 2, 3] 을 forEach 돌린 첫 번째 item = 1 을 제외한 나머지 원소를 가진 새로운 배열을 생성한다. 여기서 ... 의 의미는 배열 자체가 아닌 배열의 원소만 가져온다는 의미이며, slice 는 첫 번째 파라미터 부터 두 번째 파라미터까지의 원소를 리턴한다. 두 번째 파라미터가 없을 경우 첫 번째 파라미터의 인덱스부터 배열의 끝까지 리턴한다. 즉 현재 arr의 첫 번째 원소인 item = 1 을 제외한 나머지 원소 [2, 3] 을 가진 배열을 리턴한다.
- item = 1을 제외하고 새롭게 생성한 배열 remain = [2, 3] 으로 fnPermutation 을 재호출한다. 이 때 selectNum - 1 을 하는 이유는, 이미 처음 호출한 fnPermutation에서 첫 번째 값으로 1 을 추출해냈기 때문이다.
- [2, 3] 으로 다시한번 1의 내용을 반복한다.
- 남은 배열인 [3] 으로 fnPermuation을 재호출한다.
- selectNum = 1 이 되었으므로 [3]을 그대로 리턴한다.
- 위에서 구한 값을 합친다.
- 해당 값을 최상위 배열에 넣어준다.
4. 중복순열
기존 순열의 결과가 [1, 2] / [1, 3] / [2, 1] / [2, 3] / [3, 1] / [3, 2] 라면
위의 결과에 [1, 1] / [2, 2] / [3, 3] 이 추가된다.

기존의 순열과 달라진 점은, 본인을 제외한 나머지 배열을 생성할 필요 없이, 처음 Input 값 그대로 다시 넣어서 보내준다는 것이다. 물론 골라야 할 값은 selectNum - 1 해야만한다. 그렇지 않으면 무한루프에 빠지게 되니 조심하자.
'Programming > Javascript' 카테고리의 다른 글
| [Tip] 구글 애드센스(AdSense) Height Auto Important 강제 적용 해제 (0) | 2024.01.27 |
|---|---|
| [React] 컴포넌트(Component) Fade In/Fade Out 구현 (0) | 2022.08.03 |
| [React] 'react-scripts'은(는) 내부 또는 외부 명령 실행할 수 있는 프로그램, 또는 배치 파일이 아닙니다. (0) | 2022.08.03 |
| [Javascrit] 정규표현식 (Regular Expression) 정리 (0) | 2022.07.27 |
| [React] Modal 만들기 (React-Modal 사용 X) (0) | 2022.02.26 |




댓글